The following research lines are developed
-
Researchers
Previous Researchers: Gonzalo Suárez, Héctor Mártin, Marisel Di Pietro Martínez, Martín Giuliano.
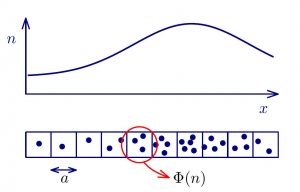
We develop a mean field approximation for the study of diffusion processes with interaction from a general perspective, applicable to different situations, such as diffusion of solute in solvent or particles adsorbed on a surface. We assume that the interaction is of short range and it can be restricted to cells of size a, as shown in the figure below; the interaction potential depends on the number of particles n in each cell.
We analyze the possible variations of the diffusion coefficient as a function of concentration.
The theory developed for the transition probabilities between neighboring cells is applied to resolve some aspects of diffusion in, for example, binary metal alloys or fluid models with hard-core or Lennard-Jones interactions.
Some publications on this line:
Mean-field approach for diffusion of interacting particles
Mean-field approach to diffusion with interaction: Darken equation and numerical validation
-
Researchers
-
Researchers
- Pamela Guruciaga
- Jose Luis Iguain
- Daniel Alejandro Martin
-
Researchers
Inspired by the interfaces which can be seen in nature, in this group we develop a simple model to describe them. We use large-scale numerical simulations implemented in graphical processing units (GPU), and then we compare the results with measurements done by colleagues from Bariloche and Paris.
Interfaces in nature
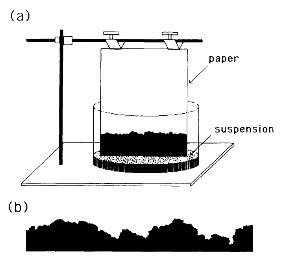
Interfaces act as frontiers between regions or faces. In nature they can be found in several scenarios, as coffee stains, wetting lines over substrates or forest fires.
Coffee stain in paper. Schematic picture from the experiment (a) and scanned paper whose width is 20 cm. [S. V. Buldyrev et al., 1992]
Wetting line over a disordered substrate. The liquid is glycerin, the substrate is glass covered with chromium patches (10×10 μm) which shine in the dry areas. [S. Moulinet, LPS Paris]
Forest fire in Sabangau (2015) [Foto de OuTrop]
En el campo de la física de la materia condensada, este tipo de interfases pueden hallarse tanto en los vórtices en superconductores como en los dominios magnéticos en materiales ferromagnéticos. A continuación se muestran ejemplos de mediciones en materiales ferromagnéticos por los grupos de Paris y Bariloche.
[J. Ferré, LPS Paris]
Dominio de ∼50 μm de ancho [paredom, Bariloche]
Modelo
A pesar de la amplia variedad de escalas involucradas en los ejemplos dados, la dinámica de las interfases mencionadas es similar. Si uno mide la rugosidad y la velocidad con la que se desplaza la interfase, en todos los ejemplo dados pueden observase los mismos exponentes dinámicos.
Tomando una porción correspondiente de cada sistema, la interfase puede considerarse como una línea plana (aunque rugosa). A su vez, la línea mencionada la estudiamos como compuesta por elementos unidos por resortes. Por lo tanto decimos que la línea es elástica, con resortes que tratan de “aplanarla”, retrasando a los elementos más adelantados a sus vecinos y viceversa. Por otro lado, la línea se desplaza en un medio inhomogéneo, rugoso, que por tener pozos y montañas hace que algunas partes de la interfase se retrase y otras avancen fácilmente. Además, la línea es empujada homogéneamente por una fuerza externa e, incluso, consideramos la aplicación de una temperatura como fuerza locales que actúan sobre cada elemento de manera aleatoria e independiente. De esta manera, puede escribirse la siguiente ecuación que resume el modelo que implementamos en nuestra investigación
Así estudiamos la velocidad y la rugosidad, entre otros observables, para describir la dinámica.
En cuanto a las mediciones experimentales, buscamos describir en particular lo que se observa para los dominios magnéticos mencionados en los ejemplos. En ellos se mide la velocidad, en la que pueden observarse distintos regímenes en función del campo externo y la temperatura aplicadas.
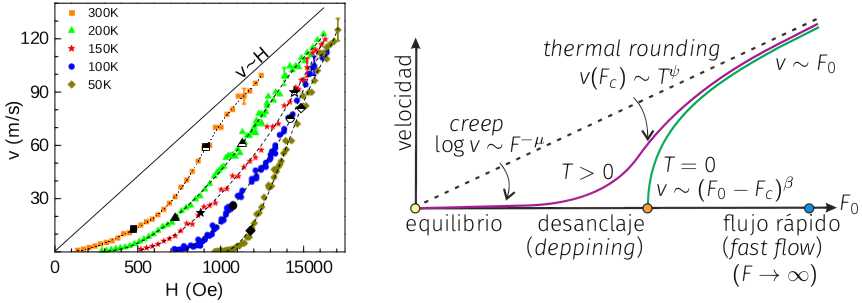
Velocidad de la pared de dominio en una película delgada de Pt/Co(0.45 nm)/Pt [Gorchon et al., 2014] y regímenes observados.
Lastest publication: https://link.aps.org/doi/10.1103/PhysRevE.96.022112 -
Researchers
- Miguel Hoyuelos
- Pablo Sisterna
The study of diffusion with interaction has had a derivation in another field: quantum statistics. A frequent problem is to analyze how the diffusion coefficient behaves as a function of the interaction between particles; that is, we know the interaction and we want to know the diffusion coefficient. A not so frequent, but also interesting, problem is the inverse one: we know the diffusion coefficient and we want to know the interaction that, in turn, gives us the equilibrium distribution of the particle number. If we assume a free diffusion coefficient, independent of the concentration, we must obtain absence of interaction, and Maxwell-Boltzmann statistics. Using a mean field theory developed in Phys. Rev. E 92, 062118 (2015), we obtain, in the case of free diffusion, not only the Maxwell-Boltzmann statistic, but also that of Bose-Einstein and Fermi-Dirac. That is, the hypothesis of free diffusion coefficient in the energy space can be taken as an alternative method for deriving quantum statistics. There is also a fourth statistic, which we call ewkons, which, given the thermodynamic characteristics of a gas of ewkons, could be useful for the description of dark energy
Publications:
Quantum statistics of classical particles derived from the condition of a free diffusion coefficient
